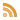Menschliche Potenzprobleme |
... und was das mit unser aller Leben zu tun hat |

Ja, klar. Titel und Artikelbild sind reines Clickbaiting. Doch wenn dieser Artikel dadurch mehr Aufmerksamkeit erfährt, so hat er es verdient ;-) Denn es geht um die Fähigkeit des Menschen, mathematische Potenzen zu beurteilen. Oder eben die Nicht-Fähigkeit. Ein sehr wichtiges und ebenso vernachlässigtes Thema in Pandemie- und Klimawandel-Zeiten – mehr darüber weiter unten. Also bitte nicht gleich weglaufen, wenn du Mathe hasst.
Der Mensch kann Additionen verstehen. Die berühmten Äpfel und Birnen kann er problemlos addieren und subtrahieren. Drei Äpfel plus fünf Äpfel – alles kein Problem, auch wenn es mal dreißig Äpfel und fünfzig Äpfel werden. Danach allerdings wird es schon schwieriger. Spätestens wenn es in den Hunderterbereich geht, fehlt dem Menschen die Anschauung. Hundert Dinge abzuschätzen geht schon ziemlich oft schief.
Schon in der Grundschule lernen wir auch das Malnehmen, die Multiplikation. Hier ist es schon gar nicht so leicht, den Vorgang zu veranschaulichen. Drei mal sechs Äpfel – na gut, das funktioniert noch mit drei gefüllten Obstschalen. Doch die Anschauung bleibt hier schon bei den zweistelligen Zahlen auf der Strecke. Acht mal zwölf Äpfel – niemand hat schon einmal acht Obstschalen mit je zwölf Äpfeln gesehen, jedenfalls nicht im Grundschulalter. Verstehen, begreifen und veranschaulichen kann man den Vorgang der Multiplikation nur im einstelligen Bereich. Sicher, wer die drei mal sechs Äpfel verstanden hat, der kann auch mit höheren Zahlen umgehen, aber nur auf rein mathematik-mechanische Art und Weise, nicht mehr mittels des Verstehens.
Tja, und dann gibt es zu allem Überfluss auch noch das Potenzieren, das deutlich nach der Grundschulzeit gelehrt wird. Während die Multiplikation mehrere Additionen zu einer kurzen Rechenvorschrift zusammenfasst (3 + 3 + 3 + 3 + 3 = 5 x 3), so fasst das Potenzieren mehrere Multiplikationen zusammen: 3 x 3 x 3 x 3 x 3 = 35 (drei hoch fünf). Doch bereits hier versagt unsere Vorstellung vollständig (Mathe-Genies ausgeschlossen), Äpfel haben hier jedenfalls ausgedient. Für drei hoch fünf fällt mir kein anschauliches Beispiel aus einem normalen Lebensalltag ein. In den Wissenschaften dagegen gibt es Potenzen noch und nöcher.
Zum Beispiel in der Zehnerpotenz-Schreibweise (wer keinen Bock auf etwas Mathematik hat, überspringe die folgenden drei Abschnitte). Besonders in der Naturwissenschaft, wo vielfach mit winzigen und riesigen Zahlen hantiert werden muss, wird mit Zehnerpotenzen gearbeitet: 10 = 101 (zehn hoch eins) ist dabei die Grundlage. 100 = 10 x 10 = 102 ist der nächste Schritt und die zweite Zehnerpotenz, 1.000 = 10 x 10 x 10 = 103 die dritte u.s.w.. Für die nullte Potenz gilt: 100 = 1, das muss der Nicht-Mathematiker hier einfach mal glauben. Die Nicht-Mathematikerin auch. Dann gibt es noch die negativen Potenzen (10-1 = 0,1 ...), um die es hier aber nicht gehen soll, ganz zu schweigen von den nicht-ganzzahligen. Im Überblick sieht das so aus:
...0,001=10-3(ein Tausendstel)0,01=10-2(ein Hundertstel)0,1=10-1(ein Zehntel)1=10010=101100=1021.000=1031.000.000=106(eine Million)1.000.000.000=109(eine Milliarde)...
Um alle möglichen Dezimalzahlen darstellen zu können, wird diese Zehnerpotenz üblicherweise mit einer beliebigen Zahl (oft mit genau einer Stelle vor dem Komma) multipliziert. Man kann sich merken, dass dabei das Komma der Zahl vor der Zehnerpotenz einfach um so viele Stellen verschoben wird, wie die Zehnerpotenz (die Hochzahl / der Exponent) anzeigt (positive Exponenten nach rechts, negative nach links):
1,2x101=126,43x103=64309,33026x104=93302,63,1415x100=3,14157,4x10-4=0,00074
In Wissenschaft und Technik ist es unumgänglich, sich das Leben auf diese Weise zu vereinfachen. Denken wir nur an das Licht, eine elektormagnetische Schwingung. Gelbes Licht schwingt mal eben so mit 510 Terahertz, also 510x1012 = 5,1x1014 = 5,1 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 mal pro Sekunde. Der Vorteil der Zehnerpotenz-Schreibweise wird schon in diesem gemäßigten Beispiel mehr als deutlich. Der Verzicht auf das Potenzieren als Vereinfachung von Multiplikationen würde ellenlange Rechenvorschriften nach sich ziehen. Würde ich auch noch auf die Multiplikation als Vereinfachung von Additionen verzichten, müsste ich die Anzahl der Schwingungen pro Sekunde sogar schreiben als: 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + ..., oder sagen wir 100 + 100 + 100 + 100 + 100 + 100 + 100 + 100 + ... – ich müsste 5,1x1012 Summanden aufschreiben, also 5100 Milliarden, was vermutlich die Kapazität des mir zugewiesenen Serverspeicherplatzes dieser Website sprengen würde.

Apropos Milliarden (hier sollten Mathe-Phobiker wieder einsteigen): Nicht nur die wissenschaftliche Welt macht sich das Leben leichter. Auch im alltäglichen Umfeld haben wir uns Abkürzungen für hohe Zahlen zugelegt. Das Wort Million zum Beispiel, das 106 = 10 x 10 x 10 x 10 x 10 x 10 bezeichnet. Eine Milliarde ist 109 = 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10. So können wir die deutsche Bevölkerung kurz mit rund 80 Millionen beziffern und die der Welt mit 8 Milliarden. Genaugenommen ist schon unser Dezimalssytem eine solche Vereinfachung. Jede Stelle einer Zahl hat dabei nicht einfach ihren eigenen Wert, sondern wird insgeheim mit dem Stellenwert der Position multipliziert, an der sie steht (Stellenwertsystem). Die Dezimalzahl 5147 ist also die Summe vierer Multiplikationen: 5x1000 x 1x100 + 4x10 + 7x1 = 5000 + 100 + 40 + 7 = 5147 (es ist schon ein wenig verrückt, das Dezimalsystem mittels Dezimalschreibweise zu demonstrieren). Die Römer hätten mit ihrer rein additiven Zahlschrift noch MMMMMCXLVII schreiben müssen. Sowohl das Dezimalsystem als auch die Abkürzungen wie Million oder Milliarde funktionieren gut und bringen uns im Alltag auch weiter. Allein: Wir verstehen nicht mehr, was wir sagen, und schlimmer noch: Wir merken es nicht einmal.
Besonders ärgerlich ist das in Finanzangelegenheiten. Besagte Römer mussten für die Bezahlung großer Werte noch mit einer Goldkiste anrücken. Kostete etwas zehnmal so viel, brauchte man schon eine Kutsche mit zehn solcher Kisten. War es hundertmal so teuer, brauchte man genau zehn solcher Kutschen. Kostete etwas tausend mal so viel, dann ... Wie ihre Schrift war auch ihr Geld ein reines Additionssystem. Sehr unpraktisch. Doch ein Mehr an Wert schlug sich direkt nieder in einem Mehr an Goldgewicht, was ein unmittelbares Gefühl für den Wert vermittelte. Mit dem Aufkommen bestimmter Münzwerte änderte sich das, und noch viel später, beispielsweise bei der Geburt der D-Mark, konnte man 50 D-Mark mit einem einzelnen Schein bezahlen, 100 oder 1000 D-Mark aber ebenso (auch eine Art Stellenwertsystem). Erst bei noch größeren Werten kam dann der Geldkoffer ins Spiel (wieder ein reines Additionsverfahren). Heute bezahlt man per Onlinebanking. Haptisch hat man hier gar nichts mehr „zu begreifen“. Man tippt vier Ziffern, klickt auf ein paar Buttons und ist mal eben einen Monatslohn los. Das meine ich mit ärgerlich.
Wir sehen: Hat man es mit großen Zahlen zu tun, dann ist es eigentlich wichtig, sie verstehen und einschätzen zu können. Die menschliche Fähigkeit dazu ist aber sehr begrenzt. Ab der Hundert fehlt uns die Anschauung, die Multiplikation ist eher ein theoretisches Wissen, und für die Potenzierung haben wir gar keinen Sinn. Große Zahlen, Multiplikation, Potenzierung – dumm, dass alle drei Dinge das moderne Leben bestimmen.
Wer versteht die Bedeutung von 500kg maximalen Gewichts in einem Aufzug? Ich meine wirklich, anschaulich verstehen, wer hat schon mal 500kg gehoben? Wer hat eine Vorstellung von dem ungeheuen Zeitraum der 2.022 Jahre seit Christi Geburt? Wer kann sich die 30.000-köpfige Bevölkerung einer Kleinstadt vorstellen? Wer kann ermessen, was es heißt, wenn unter der NS-Herrschaft 165.000 aus Deutschland stammende Juden ermordet wurden? Wer begreift es, wenn die Zahl der ermordeten polnischen Juden etwa 20 mal so hoch beziffert wird (beides von der Bundeszentrale für Politische Bildung)? Wer versteht den Preis einer Villa für 3,5 Mio Euro, wer die 100 Milliarden, die 2022 für die Bundeswehr bewilligt wurden? Und kann es wirklich sein, dass alle 2,5 Milliarden Smartphones auf der Welt, wenn sie gleichzeitig geladen werden, 50 Gigawatt Leistung benötigen, obwohl jedes einzelne nur mickrige 20 Watt zieht? Das sind 35 mittlere Atomkraftwerke á 1.400 Megawatt. All das ist ziemlich unbegreifbar. Wir können uns die Zahlen merken, weil wir vereinfachende, abkürzende Zahlen- und Benennungssysteme erfunden haben, aber erfassen können wir die Mengen nicht. Und doch müssen wir damit umgehen.
Und das Potenzieren setzt Allem die Krone auf: Wie sollten wir begreifen, dass sich ein Vermögen von 1.000€ bei winzigen (wenn auch utopischen) 2% Zinsen nach 35 Jahren verdoppelt (Zinseszinsrechnung: 1.000 x 1,0235 = 1.999,89)? Wer hat sich verinnerlicht, warum eine mickrige Corona-Inzidenz von 10, die sich alle zwei Wochen verdoppelt, nach vier Monaten bei 2.560 liegt und nach nur einem weiteren Monat schon bei über 10.000? Und das, nachdem sich über die ersten Monate hinweg kaum etwas verändert. Ach ja, und dann gibt es da noch die Geschichte mit den Weizenkörnern auf dem Schachbrett (Weizenkornlegende): Auf dem ersten der 64 Schachbrett-Felder ein Weizenkorn, auf dem zweiten zwei, auf dem dritten vier, dann 8, 16, 32 ... Allein auf dem letzten Feld lägen 263 ≈ 9x1018 = 9 Trillionen Körner und eine Masse von etwa 370 Milliarden Tonnen. Keine klare Vorstellung von dieser Menge? Ich auch nicht. Vielleicht hilft es zu wissen, dass man fast 300 Milliarden Jahre daran zählen würde (ein Korn pro Sekunde).
Warum schreibe ich all diese Zahlenspielchen auf? Der Untertitel meines Blogs lautet: „Für mehr Bewusstsein“. Ich möchte das Bewusstsein dafür schärfen, dass wir große Zahlen und mathematische Naturgesetzmäßigkeiten wie das Potenzieren einfach nicht verstehen können. Na und? Nun, gleichzeitig benehmen wir uns so, als könnten wir es.
- Ein Blick in die jüngere Vergangenheit: Wir glauben nicht etwa dem Epidemiologen, der vor einer Überlastung des Gesundheitssystems in einigen Wochen warnt, sondern lieber unserem Bauchgefühl, das nur eine aktuell winzige Inzidenz wahrnimmt. Gern haben wir uns damals vielfach selbst als Experten angesehen, obwohl wir keine Ahnung von Potenzierung (exponetielles Wachstum) haben.
- Im Jahr 2020 habe ich mehrfach die Frage gehört: „Kennst du auch nur einen einzigen Corona-Fall? Also ich jedenfalls nicht.“ Und dann folgte oft: „Vielleicht gibt es Corona gar nicht.“ – für mich ein klares Zeichen dafür, dass nicht einmal der Inzidenz-Begriff („Soundsoviel Neuerkrankungen pro Woche und pro 100.000 Einwohner“) verinnerlicht wurde. Ich glaube nicht, dass ich 10.000 Personen kenne, nicht einmal 1.000, wie sollte ich da bei einer Inzidenz von 10 während der Corona-Anfangszeit auch nur einen Betroffenen kennen? Um das wie selbstverständlich zu verstehen, müssten wir ein Gefühl für große Zahlen haben. Haben wir aber nicht.
- Wer hat je den Begriff „Bevölkerungsexplosion“ verstanden? Für wen ist anschaulich klar, dass bei einer winzigen Steigerungrate von unter 2% jährlich die Bevölkerungszahl von Deutschland, also grob 80 Mio Menschen, zur Weltbevölkerung hinzukommt? Wer versteht die Bedeutung der Tatsache, dass sich die Weltbevölkerung von 1975 an etwa verdoppelt hat? (Quelle: Uno-Zahlen via Wikipedia)
- Bereits 1972(!) veröffentlichte der Club of Rome seine Studie „Die Grenzen des Wachstums“ (The Limits to Growth). Darin wurde mit modernsten Mitteln (Computersimulationen auf Großrechnern) ermittelt, wie sich die Welt in den kommenden Jahrzehnten verändern wird, und zwar in Bezug auf Kerngrößen wie Weltbevölkerung, Industrialisierung, Ressourcen, Ernährungszustand, Umweltzerstörung, ... Sehr kurz zusammengefasst lautete das Ergebnis: Verläuft alles wie bisher (1972), dann ist bis spätestens 2100 ein Zusammenbruch des bestehenden Wirtschaftssystems zu erwarten, einhergehend mit einem drastischen Rückgang der Weltbevölkerung (ein Euphemismus; eigentlich: Massensterben). Allen Interessierten lege ich dringend ans Herz, wenigstens den Wikipediaartikel dazu zu lesen. In dieser Studie wurden einige Größen als exponentiell steigend angenommen. So etwa das Wirtschaftswachstum, das, mit beispielsweise „gesunden“ 3% angegeben, ein exponentielles Wachstum beschreibt – was aber kaum jemand wirklich als solches begreift. Wer hat dieser wissenschaftlichen Studie geglaubt? Niemand, könnte man annehmen, denn ein (in der Studie dringend angeratenes) Umdenken blieb weitgehend aus. Nachträgliches Zurückrechnen – beispielsweise im 30-Jahre-Update von 2004 – hat ergeben, dass tatsächlich alles sehr ähnlich verlaufen ist, wie im „busyness-as-usual“-Szenario der Studie vorhergesagt. Politik und Bevölkerung haben alles einfach weiterlaufen lassen, teilweise bis heute. Ich glaube nicht, weil es ihnen egal war, was sie ihren Nachkommen hinterlassen würden, sondern weil sie es einfach nicht geglaubt haben. Zu gesund sah es damals aus in der (Wirtschafts-)Welt, zu klein waren die Veränderungen zum Schlechten (wie bei exponentiellen Vorgängen üblich in deren Anfangszeit).
- Im Jahr 2018 begann die Schwedin Greta Thunberg ihre Schulstreiks für das Klima, aus denen die weltweite Bewegung „Fridays for Future“ hervorging. Ausgerechnet eine gerade einmal 15-Jährige schien damals verstanden zu haben, wie exponentielle Vorgänge unsere Welt gefährden. Exponentielle Vorgänge beim Klimawandel? Ich empfehle hierzu den Artikel „Auch die Treibhausgase wachsen exponentiell“ im Schweizer Magazin „Republik“. Fridays for Future jedenfalls forderte ein, was eigentlich seit Anfang, spätestens seit Mitte des 20. Jahrunderts hätte geschehen müssen: Die drastische Reduzierung der Treibhausgasemissionen. So machte bereits 1906 der schwedische Physiker und Chemiker Svante Arrhenius (seine Mutter war übrigens eine geborene Thunberg) verhalten auf den menschenverursachten Temperaturanstieg durch CO2 aufmerksam. Für genauere Berechnungen fehlten ihm jedoch zuverlässige Daten. Diese lieferten Ende der 1950er Jahre der junge Chemiker Charles David Keeling und viele andere. Die in der Folge immer wieder angestellten Berechnungen und Voraussagen, dass sich das Klima dramatisch erwärmen wird, wurden – eigentlich bis Greta Thunberg – verdrängt oder ignoriert. Weil niemand, außer einigen naturwissenschaftlich-mathematischen Überfliegern, die Zusammenhänge verstanden oder auch nur glaubten.

Dies alles als Grundlage plädiere ich hier für mehr Wissenschaftsgläubigkeit. Ich rufe dazu auf, das eigene Empfinden, das eigene Gefühl für Vorgänge und Zusammenhänge in der Natur hintenanzustellen, wenn es um wichtige, womöglich globale Handlungsentscheidungen geht. Wer bin ich, Aussagen eines Immunulogen Drosten infrage zu stellen? Wie sollte ich eine „Meinung“ haben zur Notwendigkeit des Verzichts zu Gunsten unserer Lebensgrundlagen? Ich habe – wie auch sonst alle Menschen – keinerlei vertrauenswürdiges Gefühl für Zahlen, insbesondere nicht für die in der Naturwissenschaft üblichen riesigen oder winzigen Zahlen, genausowenig für exponentielle Vorgänge und komplizierte, naturwissenschaftliche Zusammenhänge und Regelkreise. Facebook übrigens auch nicht. Daher vertraue ich lieber denen, die von Haus aus das meiste Zeug dazu haben, nüchtern und sachlich mit Zahlen zu hantieren und aussagekräftige Ergebnisse zu erarbeiten – durch Rechnen statt durch Meinen.
Mir ist bewusst, dass die Unfähigkeit des Menschen, Zahlen und numerische Entwicklungen zu beurteilen, nicht der einzige Grund dafür ist, dass Entscheidungen verschlafen werden. Bequemlichkeit, Stolz und die Unfähigkeit, sich für Verzicht zu entscheiden, sind weitere Gründe. Doch gerade die Pandemie, die Hauptinspiration zu diesem Artikel, hat mir gezeigt, wie sehr Zahlen unser Leben bestimmen. Unser Bauchgefühl hilft uns wohl im sozialen Zusammenleben weiter, in Sachen Zahlen aber sind wir damit absolut aufgeschmissen. Das ist nicht schlimm. Schlimm ist es, wenn man es nicht weiß – oder nicht wahrhaben will.
| Die Grenzen des Wachstums Club of Rome, 1972 | https://www.library.dartmouth.edu/digital/digital-collections/limits-growth |
| Die Grenzen des Wachstums Wikipedia | https://de.wikipedia.org/wiki/Die_Grenzen_des_Wachstums |
| Fridays for Future | https://de.wikipedia.org/wiki/Fridays_for_Future |
| Auch die Treibhausgase wachsen exponentiell im Schweizer Magazin „Republik“ | https://www.republik.ch/2020/03/23/auch-die-treibhausgase-wachsen-exponentiell |
| Svante Arrhenius, Chemiker Wikipedia | https://de.wikipedia.org/wiki/Svante_Arrhenius |
| Charles Keeling, Klimaforscher Wikipedia | https://de.wikipedia.org/wiki/Charles_David_Keeling |
| am 24.10.2022 um 15:08 Uhr | Hallo, vielen Dank für diesen interessanten Beitrag. Wieder ein sehr spannendes Thema! Hast mir auf jeden Fall geholfen. Danke dir. Ich freue mich auf weitere interessante Beitrage von dir! Beste Grüße Graffitiartist |
| am 22.05.2023 um 20:54 Uhr | Toller Artikel und gerade in der heutigen Zeit auch sehr wichtig. Die limitierte Vorstellungskraft des Menschen lässt ihn an großen Zahlen verzweifeln. Auch Relationen wie die Inzidenz ist für viele Menschen schwer begreiflich. Richtig spannend wird es dann beim Begriff von "Unendlichkeit"... |
Grundsätzlich mache ich hier keine Produktwerbung. Und auch jetzt geht es mir nicht um die Marke, sondern um das Prinzip: Der Einhandmischer, bei dem die Mittelstellung kaltes Wasser liefert. Ich selbst habe so einen von der Firma hansgrohe, die den CoolStart auf den Markt gebracht hat. Für mich eine der wichtigsten Erfindungen neuerer Zeit.